6-1. СЕМЬ ДРОБЕЙ
Найдутся ли семь различных правильных несократимых дробей со знаменателями от 2 до 6 и с суммой 4?

6-5, 7-5. РАВНЫЕ КУСКИ
Некоторые клетки доски размером 7х7 покрашены в чёрный цвет, образуя чёрный многоугольник. Его разрезали по прямой, идущей по линии сетки. Мог ли он распасться на пять равных фигур?

6-6, 7-6. ТЁЗКИ
Ученики писали олимпиаду в двух залах. Ни в одном из залов не было трёх тёзок. У 100 учеников были два тёзки в другом зале. У 144 учеников было хотя бы по одному тёзке в каждом зале. У скольких учеников было ровно по одному тёзке в каждом зале? (Напомним, что тёзками считаются люди с одинаковыми именами.)

6-1. ПОЛУЧИТЬ 2020
Найдётся ли шестизначное число, кратное 31, из которого можно удалить две одинаковые цифры и при этом получить 2020?

6-6. КОРОБКИ
В ряд стоят семь коробок, в которых по порядку лежат 1, 2, 3, 4, 5, 6 и 7 орехов. За один шаг можно выбрать любые две коробки А и Б, подсчитать общее количество орехов в коробках, стоящих между ними, и такое количество орехов перенести из А в Б. Можно ли за несколько шагов сделать так, чтобы во всех коробках орехов стало поровну?

6-7, 7-7. СТОИМОСТЬ ОБЕДОВ
Цена стандартного обеда в таверне «Буратино» зависит только от дня недели. Аня обедала 10 дней подряд, начиная с 10 июля, и заплатила 70 сольдо. Ваня также заплатил 70 сольдо за 12 обедов, начиная с 12 июля. Таня заплатила 100 сольдо за 20 обедов, начиная с 20 июля. Сколько заплатит Саня за 24 обеда, начиная с 24 июля?

7-3. ЦВЕТНЫЕ КУБИКИ
У Саши было четыре раскрашенных кубика. Расставляя их по-разному, он по очереди сфотографировал три фигуры (см. рисунок сверху). Затем Саша сложил из них параллелепипед размером 2 × 2 × 1 и сделал его черно-белое фото (см. рисунок снизу). Все видимые на фото грани кубиков одного и того же цвета. Какого?

6-3. ПЕРЕПРАВА
На левом берегу реки собрались 5 физиков и 5 химиков. Всем надо на правый берег. Есть двухместная лодка. На правом берегу ни в какой момент не могут находиться ровно три химика или ровно три физика. Каким образом им всем переправиться, сделав 9 рейсов направо? (Если человек приплыл к берегу в лодке и, не высаживаясь, уплыл обратно, он на этом берегу не считается)

6-6. ОДНОКЛАССНИКИ
На кружок пришли дети из двух классов: Ваня, Дима, Егор, Инна, Леша, Саша и Таня. На вопрос: «Сколько здесь твоих одноклассников?» каждый честно ответил «Двое» или «Трое». Но мальчики думали, что спрашивают только про мальчиков-одноклассников, а девочки правильно понимали, что спрашивают про всех. Кто Саша – мальчик или девочка?

7-5. ПЕСТИКИ – ТЫЧИНКИ
Артемон подарил Мальвине букет из аленьких цветочков и черных роз. У каждой черной розы 4 пестика и 4 тычинки, а на стебле 2 листка. У каждого аленького цветочка 8 пестиков и 10 тычинок, а на стебле 3 листка. Листков в букете на 108 меньше, чем пестиков. Сколько тычинок в букете?

6-3. ОРЕХИ
В ряд стояло 10 детей. В сумме у девочек и у мальчиков орехов было поровну. Каждый ребёнок отдал по ореху каждому из стоящих правее его. После этого у девочек стало на 25 орехов больше, чем было. Сколько в ряду девочек?

6-5. РАВЕНСТВО
Может ли в равенстве 1/x = 1/y + 1/z одно из чисел x, y, z быть однозначным, другое – двузначным, третье – трёхзначным?

7-4. ЧИСЛОВОЙ КРУГ
Незнайка хочет записать по кругу 2015 натуральных чисел так, чтобы для любых двух соседних чисел частное от деления большего на меньшее было простым числом. Знайка утверждает, что это невозможно. Прав ли Знайка?

6-5. УГОЛКИ
УГОЛКИ На клетчатой доске размером 4×4 Петя закрашивает несколько клеток. Вася выиграет, если сможет накрыть все эти клетки не пересекающимися и не вылезающими за границу квадрата уголками из трёх клеток. Какое наименьшее количество клеток должен закрасить Петя, чтобы Вася не выиграл?

6-6. КАНАТНАЯ ДОРОГА
К кабинке канатной дороги, ведущей на гору, подошли четыре человека, которые весят 50, 60, 70 и 90 кг. Смотрителя нет, а в автоматическом режиме кабинка ездит туда-сюда только с грузом от 100 до 250 кг (в частности, пустой она не ездит), при условии, что пассажиров можно рассадить на две скамьи так, чтобы веса на скамьях отличались не более, чем на 25 кг. Каким образом все они смогут подняться на гору?

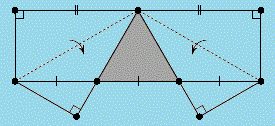
7-7. УШИ ПРЯМОУГОЛЬНИКА
Два угла прямоугольного листа бумаги согнули так, как показано на рисунке. Противоположная сторона при этом оказалась разделенной на три равные части. Докажите, что закрашенный треугольник – равносторонний.

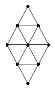
6-2. РОМБ.
Из 16 спичек сложен ромб со стороной в две спички и разбит на треугольники со стороной в одну спичку (см. рисунок). А сколько спичек потребуется, чтобы сложить ромб со стороной в 10 спичек, разбитый на такие же треугольники со стороной в одну спичку?

6-3. ТРЕУГОЛЬНИК.
Города A, B и C вместе с соединяющими их прямыми дорогами образуют треугольник. Известно, что прямой путь из A в B на 200 км короче объезда через C, а прямой путь из A в C на 300 км короче объезда через B. Найдите расстояние между городами B и C.

6-9. ДВОРЕЦ.
План дворца шаха – это квадрат размером 6×6, разбитый на комнаты размером 1×1. В середине каждой стены между комнатами есть дверь. Шах сказал своему архитектору: «Cломай часть стен так, чтобы все комнаты стали размером 2×1, новых дверей не появилось, а путь между любыми двумя комнатами проходил не более, чем через N дверей». Какое наименьшее значение N должен назвать шах, чтобы приказ можно было выполнить?

6-4,7-2. НЕЧЕСТНЫЕ ПРЯМЫЕ.
Пусть на плоскости отмечено несколько точек. Назовем прямую нечестной, если она проходит ровно через три отмеченные точки, и по разные стороны от нее отмеченных точек не поровну. Можно ли отметить 7 точек и провести для них 5 нечестных прямых?

6-6. БОЧКА ВАРЕНЬЯ И КОРЗИНА ПЕЧЕНЬЯ.
Малыш и Карлсон съели бочку варенья и корзину печенья, начав и закончив одновременно. Сначала Малыш ел печенье, а Карлсон – варенье, потом (в какой-то момент) они поменялись. Карлсон и варенье, и печенье ел в три раза быстрее Малыша. Какую часть варенья съел Карлсон, если печенья они съели поровну?

7-5. ДВАЖДЫ ПРЯМОЙ.
В треугольнике ABC на стороне AB выбрана точка K и проведена биссектриса KE треугольника AKC и высота KH треугольника BKC. Оказалось,что угол EKH – прямой. Найдите BC, если HC=5.

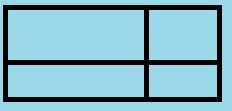
6-3. НЕЧЁТНЫЕ ПРЯМОУГОЛЬНИКИ.
На рисунке справа можно найти 9 прямоугольников. Известно, что у каждого из них длина и ширина – целые. Сколько прямоугольников из этих девяти могут иметь нечетную площадь?

6-5, 7-3. ОДНОКЛАССНИКИ.
Одноклассники Аня, Боря и Вася живут на одной лестничной клетке. В школу они идут с постоянными, но разными скоростями, не оглядываясь и не дожидаясь друг друга. Но если кто-то из них успевает догонать другого, то дальше он замедляется, чтобы идти вместе с тем, кого догнал.
Однажды первой вышла Аня, вторым Боря, третьим Вася, и кто-то двое из них пришли в школу вместе. На следующий день первым вышел Вася, вторым Боря, третьей Аня. Могут ли все трое прийти в школу вместе?

7-8. СТРАННЫЙ КВАДРАТ.
Квадрат с вершинами в узлах сетки и сторонами длиной 2009, идущими по линиям сетки, разрезали по линиям сетки на несколько прямоугольников. Докажите, что среди них есть хотя бы один прямоугольник, периметр которого делится на 4.