А.В.Шаповалов => Задачи и подборки => Геометрия
К стереометрии лучше приучать сызмальства. Да и то сказать: живем ведь не на плоскости, а в пространстве! В раннем детстве помогает игра в кубики (в идеале – в кубики Сома). Шести- и семиклассникам вполне можно давать задачки про кубики и их развертки. В общем, к началу преподавания стереометрии пространственное воображение должно быть сформировано. И отличие пространства от плоскости лучше продемонстрировать на неожиданных примерах.
1. а) Поросенок Наф-Наф придумал, как сложить параллелепипед из одинаковых кубиков и оклеить его тремя квадратами без щелей и наложений. Сделайте это и вы.
б) А может ли Наф-Наф добиться, чтобы при этом каждые два квадрата граничили друг с другом?
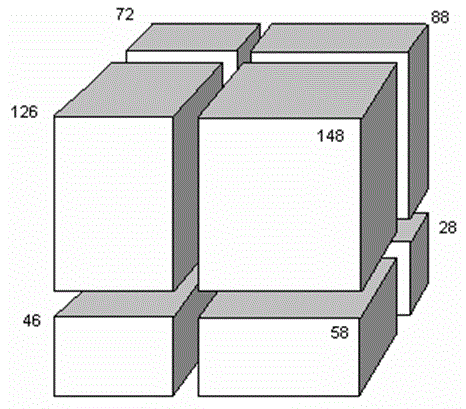
2. Деревянный брусок (прямоугольный параллелепипед) распилили (по трем пересекающимся плоскостям, параллельным граням) на восемь меньших брусков (прямоугольных параллелепипедов). На рисунке у семи брусков указана их площадь поверхности. Какова площадь поверхности невидимого бруска? 
3. Трёхмерная доска 18x18x18 состоит из кубических клеток. Параллельные граням слои считаются плоскими досками 18x18. Шахматный слон ходит по диагонали в любой из этих плоских досок. Докажите, что если слон может попасть из клетки A в клетку B, то он может сделать это не более чем за 3 хода. (М. Артемьев, К. Кноп, А. Шаповалов)
4. Можно ли кубик Рубика 8x8x8 оклеить без щелей и перекрытий прямоугольниками 1x2 так, чтобы каждый прямоугольник заклеивал ровно две клетки и у всех было
а) ровно 6 соседей?
б) одинаковое четное число соседей? (Соседи имеют общую границу ненулевой длины. Перегнутый прямоугольник может закрывать две клетки на соседних гранях.)
в)При каких натуральных n можно поверхность куба с ребром длины n оклеить без наложений и щелей бумажными прямоугольниками 1x2 так, чтобы у каждого было ровно по 5 соседей? (Прямоугольник может залезать и на несколько граней. Его стороны могут быть не параллельны рёбрам. Соседи имеют общую границу ненулевой длины).
5. Вершины замкнутой несамопересекающейся восьмизвенной ломаной совпадают с вершинами куба. Докажите, что у этой ломаной найдутся четыре звена одинаковой длины.
6. Дана замкнутая несамопересекающаяся ломаная с вершинами на ребрах единичного куба. На каждой грани все звенья параллельны между собой.
а) Может ли в этой ломаной быть не менее 12 звеньев?
б) Может ли длина ломаной быть больше 100?
7. В море плавает предмет в форме выпуклого многогранника. Может ли случиться, что 90% его объема находится ниже уровня воды, и при этом больше половины его поверхности находится выше уровня воды?
8. Докажите, что можно на каждом ребре тетраэдра записать по неотрицательному числу так, чтобы для каждой грани сумма чисел на её ребрах равнялась площади грани.
9. Есть большой куб и набор из 5 красок. Сначала Петя режет куб на меньшие кубики (размер он выбирает сам, но не более 1 см). Затем Вася красит кубики как хочет (не обязательно все одинаково), но чтобы каждая грань была одноцветна. Наконец, Петя складывает из кубиков исходный куб. Докажите, что, независимо от действий Васи, Петя может добиться, чтобы каждая грань большого куба была одноцветной.
10. а) Барон Мюнхгаузен рассказывал, как его друг Эйлер, разрезав некий картонный выпуклый многогранник по ребрам на отдельные грани, прислал их ему. Одна грань при пересылке потерялась, но барон сумел из всех оставшихся граней склеить новый многогранник большего объёма чем исходный. Может ли рассказ барона быть правдой?
б) В набор “Юный геометр” входит несколько плоских граней, из которых можно собрать выпуклый многогранник. Юный геометр Саша разделил эти грани на две кучки. Могло ли случиться, что из граней каждой кучки тоже можно собрать выпуклый многогранник?
11. От балки в форме треугольной призмы с двух сторон отпилили (плоской пилой) по куску. Спилы не задели ни оснований, ни друг друга. Могут ли спилы быть подобными, но не равными треугольниками?
12. При каких a>1 cуществует многогранник, у которого отношение площадей любых двух граней не меньше a?