А.В.Шаповалов => Задачи и подборки => Геометрия
В каждом варианте дожна быть задача по классической геометрии. Желательно нетрудная, но не упражнение.
Обычно такую задачу придумываю не я, а специалисты по геометрии. Но иногда специалистов нет, и напрягать фантазию приходится и мне.
Казалось бы, за последние 300 лет всё уже давно придумано, и не раз. А вот поди ж ты -- удаётся развернуть ситуацию так так, что ответ перестаёт быть совсем очевидным. Люблю задачи с перегибанием бумаги: и геометрия несложная, и надо построить несложную математическую модель из житейской ситуации.
1. Вершины треугольника лежат на окружности, а её центр лежит на одной из медиан треугольника (но не на стороне). Докажите, что треугольник – равнобедренный.
2. В равнобедренном треугольнике ABC с основанием AB биссектриса AL перпендикулярна медиане BM. Периметр треугольника LMC равен 30 см. Найдите периметр треугольника ABC.
3. Прямоугольный лист бумаги перегнули по прямой так, что противоположные вершины совместились. В результате получились три треугольника: в середине один двухслойный и по краям два однослойных. Докажите, что двухслойный треугольник — равнобедренный.
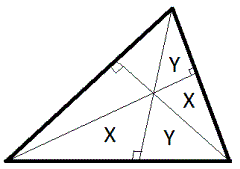
4. Три высоты остроугольного треугольника разбили его на шесть треугольников (см. рис.). Оказалось, что треугольники, отмеченные буквой Х, равны. Докажите, что треугольники, отмеченные буквой Y, тоже равны.
5. В треугольнике ABC проведена биссектриса BL. На сторонах AB и BC выбраны такие точки D и E соответственно, что биссектрисы углов ADL и CEL параллельны BL. Докажите, что прямая DE перпендикулярна BL.
6. В остроугольном треугольнике ABC сторона AB – наименьшая, M и H – точки пересечения медиан и высот соответственно. Докажите, что H лежит внутри треугольника AMB.
7. На сторонах BC, CA и AB треугольника ABC выбраны соответственно точки A', B' и C', причём медианы A'A", B'B" и C'C" треугольника A'B'C' соответственно параллельны прямым AB, BC и CA. В каком отношении точки A', B' и C' делят стороны треугольника ABC?
8.а) В выпуклом четырехугольнике ABCD биссектрисы углов B и D пересекают диагональ AC в точках K и L соответственно, AB = CD, AK = CL. Докажите, что эти биссектрисы параллельны.
б) В выпуклом четырёхугольнике ABCD биссектрисы углов B и D параллельны. Биссектриса угла B пересекает диагональ AC в точке K, а биссектриса угла D пересекает её в точке M так, что AK = CM (точки K и M различны). Докажите, что четырёхугольник ABCD — параллелограмм.
9. Бумажный треугольник со сторонами a, b, c перегнули по прямой так, что вершина, противолежащая стороне длины c, попала на эту сторону. Известно, что в получившемся четырехугольнике равны два угла, примыкающих к линии сгиба. Найдите длины отрезков, на которые делит сторону c попавшая туда вершина.
10. В прямоугольный треугольник вписали квадрат со стороной 15, две вершины попали на гипотенузу. Исходный треугольник разбился на квадрат и три меньших треугольника. Периметр одного из меньших треугольников такой же, как у квадрата. Найдите периметр исходного треугольника.
11. Постройте с помощью циркуля и линейки треугольник ABC по стороне AB и углам CBM и CAM, где M – точка пересечения медиан.
12. Докажите, что любой жесткий плоский треугольник T площади меньше 4 можно просунуть сквозь треугольную дырку Q площади 3.