S4. Lägg ihop dessa tre figurer så att de bildar en spegelsymmetrisk figur (det räcker med ett exempel).
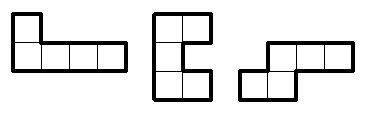
[6 poäng]
(Inom hakparenteser står den maximala poängen för varje problem. Din total poängsumma utgörs av de tre uppgifter för vilka du får flest poäng. Om du går i 8:an multipliceras din summa med 4/3, i 7:an med 3/2)
S1.
På TV 4 och kanal 5 startar en och samma film samtidigt. På TV 4 är filmen
delad i 20-minuters avsnitt med 2 minuter långa reklampauser emellan. På
kanal 5 är filmen delad i 10-minuters avsnitt med 1 minut långa reklampauser
emellan. På vilken kanal kommer filmen att sluta tidigare? Hur många minuter
tidigare?
[3 poäng]
S2. En tärning har talen 1 till 6 på sidoytorna. Tärningen kastades två gånger. Första gången blev summan av talen på de fyra lodräta sidoytorna lika med 12, andra gången lika med 15. Bestäm talet på den yta som ligger mittemot ytan med talet 3. [4 poäng]
S3. Det fanns 11 på varandra följande heltal. Man har raderat ett av talen och upptäckt att summan av de 10 tal som är kvar är lika med 2007. Bestäm det raderade talet. [4 poäng]
S4. Lägg ihop dessa tre figurer så att de bildar en spegelsymmetrisk figur (det räcker med ett exempel).
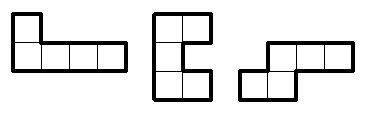
[6 poäng]
S5. På ön RGB bor endast lögnare som alltid ljuger och sanningssägare som alltid talar sanning. Under valet röstade var och en av de vuxna öborna på ett parti. När en väljare kom ut ur vallokalen ställdes det 4 frågor till denne. På frågan ”Röstade du på de Gröna?” svarade 40% ”Ja”. På samma fråga om de Röda svarade 30% ”Ja”, om de Blåa 50%, om de Gula 0%. Bestäm hur många procent av de tillfrågade som verkligen röstade på de Gröna? [7 poäng]
(Inom hakparenteser står den maximala poängen för varje problem. Din total poängsumma utgörs av de tre uppgifter för vilka du får flest poäng. Om du går i 2:an multipliceras din summa med 5/4, i 1:an med 4/3)
G1.
För roten ur 49 gäller en konstig "formel":
![]() .
Bestäm alla tvåsiffriga heltal för vilka samma formel gäller. [3 poäng]
.
Bestäm alla tvåsiffriga heltal för vilka samma formel gäller. [3 poäng]
G2. Det fanns 11 på varandra följande heltal. Man har raderat ett av talen och upptäckt att summan av de 10 tal som är kvar är lika med 2007. Bestäm det raderade talet. [4 poäng]
G3. Lägg ihop dessa tre figurer så att de bildar en spegelsymmetrisk figur (det räcker med ett exempel).
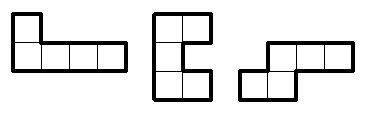
[4 poäng]
G4. Lös ekvationen:
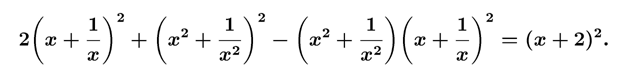
[4 poäng]
G5. På ön RGB bor endast lögnare som alltid ljuger och sanningssägare som alltid talar sanning. Under valet röstade var och en av de vuxna öborna på ett parti. När en väljare kom ut ur vallokalen ställdes det 4 frågor till denne. På frågan ”Röstade du på de Gröna?” svarade 40% ”Ja”. På samma fråga om de Röda svarade 30% ”Ja”, om de Blåa 50%, om de Gula 0%. Bestäm hur många procent av de tillfrågade som verkligen röstade på de Gröna? [5 poäng]
Y1. Vita och svarta brickor placeras på ett schackbräde. På varje rad och kolumn placeras det dubbelt så många vita som svarta brickor. Bestäm det största möjliga antalet brickor som kan placeras ut på schackbrädet på detta sätt. (I en ruta kan finnas högst en bricka). [3 poäng]
Y2.
På tavlan står talet 1 och något tal x som ej är ett heltal. Följande
spelregler är givna:
Om två stycken tal står på tavlan så får man skriva upp summan eller
differensen av dessa två tal.
Om ett tal y står på tavlan så får man skriva upp talet 1/y.
.
Man får återanvända alla tal som skrivits ner på tavlan hur många gånger man
vill.
Kan man, med enbart dessa spelregler, få talet x2 skrivet
på tavlan så småningom? [4 poäng]
Y3. ABC är en triangel (med hörnen A, B och C), AH och BK är höjderna, M är mittpunkten till sidan AB. Det visar sig att HKM är en liksidig triangel. Kan man då vara säker att även ABC är en liksidig triangel? [4 poäng]
Y4. En tabell av format 29×29 är ifylld med heltalen 1, 2, 3, ... , 29, varje heltal påträffas exakt 29 gånger. Det visar sig att summan över en huvuddiagonal är tredubbel så stor som summan under diagonalen. Bestäm talet i den centrala rutan. [6 poäng]
Y5. En trollkarl med en blindsel över ögonen ger till en åskådare 5 kort med siffrorna 1 till 5 på. Åskådaren lägger två kort i sin ficka och lämnar tillbaka resten till trollkarlens assistent. Assistenten väljer två av de återlämnade korten och åskadaren säger högt, i godtycklig ordning, vilka siffror som står skrivna på dessa. Nu ska trollkarlen avslöja vilka kort som finns i åskådarens ficka. Hur ska trollkarlen och assistenten komma överens för att tricket alltid ska lyckas? [5 poäng]
Ä1. På en datorskärm kan man se en rad av 200 personer. I själva verket består bilden av 100 stycken delar, en vuxen och ett kortare barn bredvid i varje del. Man får ändra skalan i varje del så att kroppslängderna på båda personer delas med samma heltal (skalorna i olika delarna kan ändras oberoende av varandra). Visa att man kan göra alla vuxna på skärmen längre än alla barn. [5 poäng]
Ä2. På en tavla står tre positiva tal x, y
och 1. Följande spelregler gäller:
Man får skriva upp på tavlan en summa eller en differens av två tal som redan
står skrivna.
Om ett tal z står skrivet så får man skriva upp talet 1.
Kan man, med dessa regler, alltid lyckas skriva upp:
a) talet x2? [2
poäng]
b) talet xy?
[2 poäng]
(Förtydligande. Givetvis får ett tal som redan
skrivits upp på tavlan återanvändas hur mycket man vill. Ett erhållet tal får
skrivas på tavlan även om ett sådant tal finns redan. Talen x och y
kan vara även bråktal.)
Ä3. Givet en rät linje samt två punkter А och В som ligger på samma rätvinkliga avstånd från linjen och på samma sida om linjen, hur kan man konstruera med passare och linjal en sådan punkt C på linjen att produkten АС×ВСantar det minsta möjliga värdet? (AC respektive BC betecknar här längden av sträckan från A till C respektive från B till C) [4 poäng]
Ä4. En trollkarl med en blindsel över ögonen ger till en åskådare 29 kort med talen 1 till 29 på. Åskådaren lägger två kort i sin ficka och lämnar tillbaka resten till trollkarlens assistent. Assistenten väljer två av de återlämnade korten och åskadaren säger högt, i godtycklig ordning, vilka siffror som står skrivna på dessa. Nu ska trollkarlen avslöja vilka kort som finns i åskådarens ficka. Hur ska trollkarlen och assistenten komma överens för att tricket alltid ska lyckas? [3 poäng]
Ä5. En kvadrat med sidan 1 cm delas i tre konvexa
polygoner. Kan det hända att polygonernas diametrar är högst
a) 1 cm;
[2 poäng]
b) 1,01 cm;
[2 poäng]
c) 1,001 cm?
[2 poäng]
(Polygonens diameter är det största avståndet som finns mellan polygonens
hörn).