(Inom hakparenteser stеr den maximala poängen för varje problem. Din total poängsumma utgörs av de tre uppgifter för vilka du får flest poäng. Poängtalen för delproblem adderas)
Y1. I en konvex 2002-gon har man dragit några diagonaler. Inga av diagonalerna skär varandra och tillsammans delar de 2002-gonen i 2000 trianglar. Kan det hända att alla sidor på precis hälften av dessa 2000 trianglar sammanfaller med polygonens diagonaler? [4 poäng]
Y2. Sasja och Masja tänkte var för sig på ett positivt heltal och talade om (var för sig) vilka tal de hade tänkt till Valja. Valja skrev ner talens summa på en papperslapp och talens produkt på en annan. Sedan gömde hon en av lapparna och visade den andra lappen (där råkade stå talet 2002) för Sasja och Masja. När Sasja tittade på talet sade han att han inte kunde räkna ut vilket tal Masja hade tänkt på. När Masja hörde detta sade hon att hon inte heller kunde räkna ut vilket tal Sasja hade tänkt på. Vilket tal hade Masja tänkt på? [5 poäng]
Y3. а)
En klass hade prov i matte. Det visade sig att åtminstone två tredjedelar av
uppgifter var svåra. En uppgift räknas som svår om minst två tredjedelar av
eleverna inte klarade av den. Det visade sig också att åtminstone två
tredjedelar av eleverna hade fått ett bra resultat. Med bra resultat menas att
åtminstone två tredjedelar av alla uppgifter är lösta. Är sådant möjligt?
[1 poäng]
b) Blir svaret annorlunda om man byter ut alla ”två tredjedelar” mot
”tre fjärdedelar” i problem 3a ? [2 poäng]
c) Blir svaret annorlunda om man byter ut alla ”två tredjedelar” mot ”sju tiondedelar” i problem 3a ? [2 poäng]
Y4. På ett bord ligger det 2002 kort med talen 1, 2, 3, ..., 2002. Två spelare turas om att plocka åt sig var sitt kort. Då korten på bordet tar slut räknar båda spelarna ut vad summan av talen på deras kort blir och tittar på den sista siffran i summan. Den spelaren vars sista siffra är störst vinner. Bestäm vilken av spelarna alltid kan vinna oavsett motståndarens spel, och förklara hur vinnaren måste spela. [5 poäng]
Y5. Vi har en vinkel samt en viss punkt A inuti den. Låt oss dra tre linjer genom punkt A, då korsar de vinkeln på båda sidorna och på varje sida bildar de tre skärningspunkter. Är det möjligt att dra de tre linjerna så att det på båda sidorna kommer att finnas en punkt som ligger exakt mellan (d.v.s. lika långt borta från) de andra två?[5 poäng]
(Inom hakparenteser står den maximala poängen för varje problem. Din total poängsumma utgörs av de tre uppgifter för vilka du får flest poäng. Poängtalen för delproblem adderas. )
Ä1. Sasja och Masja tänkte var för sig på ett positivt heltal och talade om (var för sig) vilka tal de hade tänkt till Valja. Valja skrev ner talens summa på en papperslapp och talens produkt på en annan. Sedan gömde hon en av lapparna och visade den andra lappen (där råkade stå talet 2002) för Sasja och Masja. När Sasja tittade på talet sade han att han inte kunde räkna ut vilket tal Masja hade tänkt på. När Masja hörde detta sade hon att hon inte heller kunde räkna ut vilket tal Sasja hade tänkt på. Vilket tal hade Masja tänkt på? [4 poäng]
Ä2.а)
En klass hade prov i matte. Det visade sig att åtminstone två tredjedelar av
uppgifter var svåra. En uppgift räknas som svår om minst två tredjedelar av
eleverna inte klarade av den. Det visade sig också att åtminstone två
tredjedelar av eleverna hade fått ett bra resultat. Med bra resultat menas att
åtminstone två tredjedelar av alla uppgifter är lösta. Är sådant möjligt?
[1 poäng]
b) Blir svaret annorlunda om man byter ut alla ”två tredjedelar” mot
”tre fjärdedelar” i problem 3a ? [1 poäng]
c) Blir svaret annorlunda om man byter ut alla ”två tredjedelar” mot
”sju tiondedelar” i problem 3a ? [2 poäng]
Ä3. Ett antal linjer är dragna genom ett plan, inga av linjerna är parallella. Linjerna delar planet i ett antal delar. I en av dessa delar har man satt ut en viss punkt A. Du har fått i uppgift att hitta en viss punkt B som ligger på den motsatta sidan av varje linje gentemot A. Visa att en sådan punkt B kan existera då och endast då delen där punkten A ligger är oändligt stor.[5 poäng]
Ä4.
Låt
x, y, z vara godtyckliga tal i intervallet
(0; p/2).
Visa olikheten
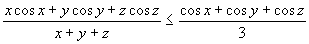
Ä5. Det finns ett oändligt talföljd bestående av positiva heltal. Alla tal i följden förutom det första får man på följande sätt: man tar det föregående talet och lägger till det en av det talets siffror, dock inte 0. Visa att det finns minst ett jämnt tal i följden. [5 poäng]