23:e Städernas Turnering, våren 2002, O-omgång

Lösningar

Y1. Eftersom både arean 99×101 och arean 49×51 är  jämnt delbart med arean ab, skulle även  SGD(99×101, 49×51) = SGD(3×3×11×101, 7×7×3×17) = 3 vara jämnt delbart med ab. Då a<b är den enda möjligheten att a=1, b=3.

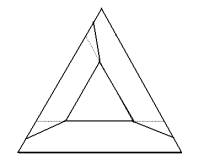
Y2. Se bilden (man ska bortse punktlinjer, de finns för att visa att delpolygoner är konvexa):

Y3. Då x³–y³ = (x²+xy+y²)(x–y) slutar även talet x³–y³ med 0. Detta innebär att både x³ och y³ har samma slutsiffra. Om ett tal a slutar med siffran 0,1,2,3, 4,5,6,7,8 eller 9 då slutar talet a³ med siffran 0,1,8,7,4,5,6,3,2 resp. 9. Observera att samtliga siffror i den andra följden är olika. Detta medför att om två heltal x³ och y³ har samma slutsiffra  måste även talen x och y ha samma slutsiffra s. För att bestämma slutsiffran till talen x²+xy+y² kan man då sätta in s istället för x och y och titta på resultatens slutsiffra.  Man får uttrycket 3s² som slutar med 0 endast om s=0. Således slutar både x och y med 0. Då slutar x²,xy,y² och även x²+xy+y² med 00.

Y4. Låt bågens KL vinkelmått är a, bågens MN är b. Beteckna med O den omskrivna cirkelns medelpunkt. Vinkeln KBL=180°–a (det kan man lätt visas genom att betrakta fyrhörningen OKBL). Fyrhörningen SKBL är inskriven omm ÐKSL=180°–Ð KBL =a. Å andra sidan ÐKSL= (ÇKL+ÇMN)/2 = (a+b)/2. Likheten a= (a+b)/2 medför att a=b. Då är även ÐMDN+ÐMSN=180°, vilket innebär att även fyrhörningen SNDM är inskriven.

Y5. a) Vi delar alla mynt i två lika stora delar och placerar de på vardera skål. Jämvikten innebär att på vardera skål har man lika många mynt av varje massa.  Då tar mynten från en av skålarna och upprepar förfarinssättet. Om jämvikten händer 7 gånger, då har man på en skål två mynt av två olika massor.

Om skålarana någång gång väger olika, ändras förfarinssättet. Man ska ta halva mynt från vardera skål och väga de mot varandra. Vid jämvikten avlägsnas de lika halvorna, kvarvarande halvor måste väga olika. Vid ojämvikten får man olika halvorna. I alla fall får mant två mynt av olika massor efter 7 vägningar.

Y5. b) Första vägningen: dela alla mynt i två lika stora grupper A och B och väga A mot B.

Andra vägningen: dela A i två lika stora grupper A₁ och A₂ och väga A₁ mot A₂.  4 fall är möjliga.

1) Jämvikt båda gånger. Då är antalet lättare mynt detsamma i A och B, dvs. 2, samt är antalet lättare mynt i A₁ och A₂ detsamma, dvs. 1. Då duger A₁ som ett sökt par.

2) Jämvikt vid den första vägningen och ojämvikt vid den andra. Då hamnade båda lättare mynt från A i en lättare delhög. Det går då att ta ett mynt från A₁ och ett mynt från A₂.

3) Ojämvikt första gången (säg A<B) och jämvikt andra gången. Då är antalet lättare mynt i A större än 2 och jämnt, dvs. 4. Man kan ta ett mynt från A och ett mynt från B.

Y6. Flygplanet var frånvarande i A. 18 timmar. Av dessa var planet 9 timmar närvarande i B. Säledes blev flygtiden 18–9=9 timmar sammanlagt, och 4,5 timmar åt båda håll.

Y7. Om S=2 eller större, blir det vänstra ledt för stor (minst 8000). Således S=1, och SAM=2002/SA. Primfaktoresering av 2002 ger oss 2×7×11×13. Då kan SA vara antingen 13 eller 14. Om SA=13 skulle SAM=154, vilket ger olika siffror för A. Då är det enda möjligheten SA=14, SAM=143.

Y8. Exempelet. Lägg två rektanglar av storlek 3×5 i två motsatta hörn vågrätt samt  två rektanglar av samma storlek i två övriga hörn lodrätt. Dela ut varje rektangel i 3 mindre rektanglar 1×5, sammanlagt blir det 12 mindre rektanglar.

Ä2. Låt oss paralleleförflytta triangeln ABC med vektorn AA´. Bilden A”B”C” (A och A” faktiskt sammanfaller) är också spegelvänd jämfört med ABC. Beteckna med l bissektrisen till vinkeln B”AB´. Vinklarna BAC och B”AC” är lika fast olika orienterade (dvs man ska vrida strålarna AB och AB” åt motsatta håll för att komma till lägena AC resp. AC”). Således är l  bissektrisen även till vinkeln C”AC”, vilket innebär att trianglarna ABC och A”B”C”  är spegelsymmetriska kring l. Då ligger mittpunkterna till sträckorna BB”, CC” samt AA” (den sista är A) på linjen l.

Ä3. Låt oss numrera bitarna i storleksordning. De treorna som innehåller biten #6 kan vara enbart 156, 146, 136, 126 eller 236 (246 passar inte ty den är tyngre än 135 pga varje respektive bit i 246 är tyngre än respektive bit i 135. De övriga fall elimineras med samma resonemang.).

Först väger vi 146 mot 235. Vid jämvikten allt är klart.

Om 146>235, desto är även 156>234. Vi väger då 136 mot 245. I fall <, = eller > kommer halvan av den  totala massan ligga i treorna 236, 136 resp.126.

Ä4. Låt oss visa att varje sätt är entydigt definierat med positioner av talen 1 och 100.

Varje sätt är i själva verket ett sätt att gå igenom alla rutor exakt en gång i tur och ordning, göra 99 drag vilka ritar ”en orm”. 1 och 100 kan vara i samma kolumn enbart vid randen, annars delas rektangel i två skilda delar. På samma sätt delar ett lodrätt drag alltid rektangeln i två skild delar, således går det bara om en av delarna är redan hellt ifylld.

Om 1 och 100 står i samma yttersta kolumn, ska man starta att gå lodrätt och får göra ett lodrätt drag endast vid motsatta randen.

Om 1 och 100 står i olika kolumner, räcker det att visa entydigheten i ett fall när 1 står i en kolumn till vänster om 100. Som sagt får man inte börja gå lodrätt. Om man går först åt höger, ska man efter ett tag gå genom samma kolumn åt vänster och då blir det omöjligt att komma tillbaka till 100 som ligger till höger. Således måste man gå först åt vänster, och får då vända om bara vid kanten och fylla  i alla rutor till vänster om 1 och i samma kolumn på entydigt sätt. Samma resonemang visar att även rutorna till höger om 100 och i samma kolumn fyllas i på ett entydigt sätt. Återstår att visa att ”ormens” huvud och svans kan sammankopplas högst på ett enda sätt då de ligger vid motsatta kolumner. Man har en rektangel kvar att fylla i. När man fyller i en hörnruta, ska man gå lodrätt, annars bildas en återvändsgränd. Då hamnar man i liknande situation fast med en mindre rektangel. I alla fall skall man fortsätta entydig ”åt höger, uppåt, åt höger, neråt” osv. och hoppas att hamna till slut i rätt vågrät rad. Således, om vi väljer två godtyckliga rutor i olika kolumner, fyller i dem med 1 och 100, då skulle det finnas antingen 1 eller 0 sätt att fylla i de övriga rutorna.

Nu är det dags att måla rutorna svart och vitt som på ett schackbräde. Man kan se att för varje sätt ska de udda talen hamna på rutor av samma färg, samma gäller de jämna talen. Bland annat ska 1 och 100 fyllas i rutor av olika färg. Låt oss visa att om vi väljer två godtyckliga rutor av olika färg samt i olika kolumner då finns det en orm som passar oss. Problemet är faktisk varför hamnar vi i rätt vågrät rad när vi fyller rektangeln mellan 1 och 100. Observera att den första ruta i rektangeln är av samma färg som ruta med 1. I en rektangeln med k kolumner gör man 2k–1 drag. Då detta antal är udda skulle den sista rutan har en färg som skiljer sig från rutan 1 och således sammanfaller med färgen hos rutan 100. Således ligger den sista rutan diagonallt gentemot 100 och i samma vågrät rad där svansen börjar.

Ä5. Det finns. Tar ett prisma med bassidorna 1 och höjden Ö3. Dess yta kan täckas med 3  regulära trianglar med sidorna 1, 2 samt 3. Den minsta täcker en bas, den största – en annan bas samt en hel sidoyta och två halvor på andra sidoytor, den tredje triangel täcker två återstående halvsidoytor.

Ä6. Om x är det minsta av de 10 talen, är övriga talen x+1, x+2, ..., x+9. En summa av 9 av dessa tal är minst x+ (x+1)+...+(x+8) = 9x+36 och högst (x+1)+...+(x+8) = 9x+45.  Av olikheter 9x+36<2002<9x+45 fås att 217⁴/₉<x<218⁴/₉ , således x=218. Eftersom summan 218+219+...+227=2225, ska man ta bort talet 2225–2002=223. Kvarstår talen 218,219,220,221,222,224,225,226,227.

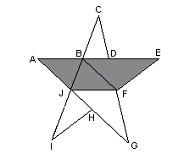
Ä7. Då skärnan är spegelsymmetrisk kring linjen AF, är trianglarna FBE och FJG kongruenta. Då skärnan  med ¹/₅ av varvet medför att trianglarna BCD, JAB samt HIJ är kongruenta. Återstår att visa att trianglarna BFJ och BAJ är kongruenta. Observera först att BDFHJ är ett regelbunden pentagonen eftersom den  övergår i sig själv vid vridningen. Då är BDF en likbent triangel, BD=DF, där vinkeln BDF=108°. Detta medför att vinkeln DBF=(180°–BDF)/2=36°. Då vinkeln FBJ=DBJ–FBD=108°–36°=72°. Men vinkeln ABJ=180°–DBJ=72°. De likbenta trianglarna ABJ och  FBJ har en gemensam bas samt lika vinklar, således de är kongruenta. Likheterna A_ABJ=A_BCD, A_BFJ=A_JIH, A_FBE = A_FJG  visar att sammantagna skuggade och oskuggade områdena har samma areor, dvs. det skuggade arean är ½.

Ä8. Exempel. Låt Pippi har avverkat 9 km varje dag på 25:e till 29 mars samt 5, 1, 6,  2, 7, 3, 8, 4 km på 30 och 31 mars samt på 1,2,3,4,5 resp. 6 april.