Y1. Lösning 1.
Vi använder triangelolikheten a+b>c samt
faktoruppdelningen
a3+b3 = (a+b)(a2–ab+b2)
(observera att båda faktorerna är positiva). Detta medför att
a3 + b3 + 3abc = (a+b)( a2–ab+b2)
+ 3abc >c( a2–ab+b2) + 3abc=c(
a2+2ab+b2)= c(a+b)2
> c3.
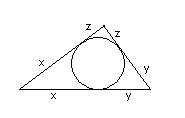
Y1. Lösning 2. För varje triangel finns positiva tal x, y, z sådana att a=y+z, b=x+z, c=x+y. (se fig.)

Vi använder bara att a>y, b>x, c=x+y:
a3 + b3 + 3abc > y3+x3+3yx( x+y) = ( x+y) 3 = c3.
Y2. Ursprungligen bildar de 4 pjäserna hörn av en rektangel med sidorna som är parallella med brädets sidor, dessutom står pjäser av samma färg på motsatta hörn. När vit gör ett drag omvandlas rektangeln till en parallelltrapets med exakt en sida som är icke-parallell med brädets sidor. Låt oss visa att svart alltid kan återställa ”rektangelläget” med sitt drag. Detta gör svart genom att förflytta pjäsen på den sneda sidan åt samma håll. Antag till exempel att vit flyttar pjäs V i sidled från ett sådant läge. Då väljer svart den pjäsen S som har varit på samma vertikal med V och flyttar den i sidled åt samma håll. Rektangelläget är återställt.
Då de vita pjäserna befinner sig på en rektangels diagonal i varje ögonblick, kan de inte hamna bredvid varandra.
Y3. Låt areorna vara n, n+1, n+2,
n+3. Då arean av fyrhörningen ABCD är 4n+6. Arean av
triangeln BCD är 4 gånger så stor som arean av triangeln ECF. Således
AABD=AABCD – ABCD <(4n+6)
– 4n = 6.
AABD=6 om triangeln ECF har den minsta arean av de alla
fyra trianglarna.
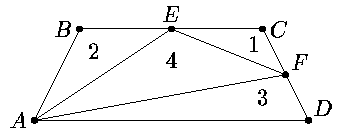
Återstår att uppvisa ett exempel. Vi tar den liksidiga parallelltrapetsen med baserna AD=6, BC=4 samt höjden 2 (talen på figuren är trianglarnas areor).
Y4. Man kan tända ”för gott” rad av n lampor för varje n utom n=1 och n=3.
Låt oss beteckna en tänd lampa med 1, en släckt lampa med 0.
Fallet n=1 är klart. I fallet n=3 ingår alla möjliga positioner i kedjorna nedanför, vilket visar att samtliga lampor släcks så småningom i alla fall:
110 -> 001 -> 010 -> 101 -> 000,
011 -> 100 -> 010 -> 101 -> 000,
111 -> 000.
Det finns ”eviglysande” positioner i alla övriga fall. Vi bildar positioner som upprepas om två minuter.
För jämna n turas om tvåor 01 och 10 i raden:
01 10 01... -> 10 01 10...-> 01 10 01...
För udda n>3 börjas raden med 10001 sedan turas om tvåor 10 och 01.
10001 10 01... ... ->01010 01 10... ->10001 10 01...
Y5. Låt oss kalla en polygon med minst tre icke-trubbiga vinklar för spetsig. En spetsig triangel är ett exempel på spetsig polygon, medan en trubbig triangel inte är en spetsig polygon. Det räcker att visa att eftersom en spetsig polygon finns från början ska den alltid finnas. Låt oss skära en spetsig polygon längs en sträcka. Pga. polygonen är konvex är vinkelsumman vid sträckans ändpunkt högst 180°. Då blir minst en av vinklarna icke-trubbig. Dessutom om vi har delat en spetsig vinkel i två delar då blir båda delvinklarna spetsiga. I alla fall utökas antalet icke-trubbiga vinklar minst med två (minst en extra vinkel vid varje ändpunkt av den skärande sträckan). Således blir det totala antalet icke-trubbiga vinklar minst 5 i två delar. Minst 3 av de vinklarna hamnar i en av delarna, som blir således en spetsig polygon.
Y6. Beteckna med kn kvoten Sn–1/an för n>2001. Enligt villkoren är kn ett positivt heltal. Låt oss visa att kn > kn+1 för varje n. Vi har
an+1kn+1 = Sn = Sn–1+an = ankn+an = an(kn+1), (1)
och eftersom an+1>an (följden an är ju växande)
skulle kn+1 > kn+1. Den sista
olikheten är ekvivalent till
kn > kn+1 då båda led är heltal.
En avtagande följd av positiva heltal kan göra enbart ändligt antal steg neråt, vilket innebär att följden når så småningom sitt minsta värde c, dvs. det finns ett nummer N sådant att för varje n > N är alla termer kn=c. Låt oss visa att c=1. Likheten (1) lyder då can+1 = an(c+1) för n > N, varav an+1 = an(c+1)/c. Detta innebär att för n > N blir talföljden en geometrisk talföljd med kvoten (c+1)/c, dvs. aN+k = aN(c+1)k/ck för godtycklig k. Då aN+k är ett heltal, är produkten aN(c+1)k jämnt delbart med ck . Då talen (c+1)k och ck är relativt primiska, är även aN jämnt delbart med ck . Detta kan var sant för ett godtyckligt k omm c=1, annars blir ck > aN . Men Sn–1 /an =c=1 precis innebär att Sn–1=an VSB.
Y7. Induktion med antalet brickor i kedjan. Vi använder varken att fälten i början och på slutet har samma antal prickar eller att uppsättningen är komplett. Det räcker att uppsättningarna är lika. Allt är klart om båda kedjor består av endast en bricka. Om vi åstadkommer att de första brickorna i kedjorna blir lika då reduceras problemet till två mindre kedjor. Vi kommer att skriva en kedja som en följd av fält. För att betona att två fält är halvor av en och samma bricka skriver vi parenteser runt ett sådant par.
Vi har en kedja 2 på formen (lb)…r, och syftar på att omvandla den till en kedja 1 på formen (la)…r, där a¹b. Om brickan (la) ligger i kedjan 2 som (al) kan vi helt enkelt vända om sträckan (lb)…(al). Nu ska vi noga betryckta fallet då (la) ligger precis i denna ordning, dvs. då kedjan 2 ser ut så här: (lb)bb1…bkl(la)aa1…amr. Betrakta då två icke-tomma mängder av antal prickar: A={a=a0, a1,…,am, r=am+1} och B={b=b0, b1,…bk} samt ett särskilt tal l. I fall när det finns ett gemensamt tal i A och B kan man vända om hela sträckan med brickan (la), vilket ger oss den ovanlösta situationen. I fall när l ingår i A kan vi omvandla situationen till en ovannämnd genom att vända om sträckan (la)…l. Återstår bara fall då A och B är disjunkta och l inte ingår i A. Då finns det bara en enda bricka av typen (lai) i kedjan 2, nämligen brickan (la). Låt oss reda ut hur talen från A och B ligger i kedjan 1. Kedjan kommer från a till r, dvs. både börjar och slutar i A, fast den måste passera genom B. Men man kan inte komma från A till B direkt, utan att passera l: i så fall skulle finnas en bricka av typen (aibj). Oavsett om denna bricka skulle ligga före eller efter (la), medför detta att A och B har ett gemensamt tal. Men om man passerar l innebär detta att alla övergångar i kedjan 1 går genom l, vilket medför att det finns minst två brickor av typen (lai). Motsägelse.Y8. Då påståendena motsäger varandra, högst ett av de kan vara sant. Om det finns exakt ett sant påstående, då är det ”Exakt 99 av påståendena på detta ark är osanna”. Antag nu att inget av påståendena är sant. Då skulle påståenden ”Exakt 100 av påståendena på detta ark är osanna” vara sann. Motsägelse. Således kvarstår den enda möjligheten, att endast det näst sista påståendet är sant.
Y9. Beteckna med g, k och m antalet gifta par, antalet kvinnor resp. antalet män på ön. Då gäller g= 2k/3 = 3m/5, varav k=3g/2, m=5g/3. Andelen gifta invånare är då 2g/(k+m) = 2g/(3g/2+ 5g/3) = 2g/(19g/6) = 12/19.
Y10.
Ä1. Utan
några restriktioner kan antas att A<B<C
. Då 0<A<p/3
gäller 0<tanA<√3. Då tanA är ett positivt heltal, är det lika med 1, A=p/4.
Då B+C=3p/4, medför detta
att
–1=tan(B+C)
= –(tanB+tanC)/(1–tanB×tanC), tanB+tanC = tanB×tanC
– 1 , (tanB – 1)( tanC – 1) = 2.
Ä2. Låt t=100. Punkt B med koordinater (t, c), där c=t3+t+1, ligger givetvis på grafen till y=x3+|x|+1.
Betrakta nu ett positivt tal r=c1/3–t. Då (t+r)3=c, ligger punkten A med koordinater (t+r, c) på grafen till y=x3.
Avståndet AB är lika med r. Å andra sidan, likheten (t+r)3=c=t3+t+1 medför att 3t2r+3tr2+r3=t+1, 3t2r < t+1, r < (t+1)/(3t2) = 101/(3×100×100) < 1/100.Anmärkning. En lösning med approximativa värden till koordinater eller avstånd går inte som ett stringent bevis. Det går dock att omvandla till ett bevis om man byter approximativa likheter till ”stringenta” olikheter. Man få till exempel uppvisa någon stringent uppskattning till feltermer.
Ä4. Beteckna med L personen som ska till den yttersta platsen till vänster. Låt oss kalla ett platsbyte för säkert alla utom möjligen L hamnar på fel plats. Vi försöker att flytta L till sin plats genom enbart säkra platsbyten. Detta skulle göras i flera omgångar. Vid varje omgång ska vi flytta L ett steg åt vänster.
Vi har raden ... V3 V2 V1 L ...., där med Vi betecknas personer till vänster om L. Om platsbytet V1<–>L är säkert gör vi detta. Annars ska V1 till platsen upptagen av L. Om då platsbytet mellan V2<–>V1 är säkert, gör vi detta, sedan byter V2<–>L. Observera att V2 hamnar då på fel plats ty den platsen tillhör V1. Om både platsbyten V2<–>V1 och V1<–>L är osäkra medan platsbytet V3<–>V2 är säkert gör vi i tur och ordning platsbytena V3<–>V2, V3<–>V1, V3<–>L, o.d. I ett allmänt fall hittar vi det närmaste säkra platsbytet Vi<–>Vi–1 till vänster om L och flyttar Vi åt höger till den byter plats med L. Vid platsbytet Vi<–>Vi–1 hamnar Vi på fel plats eftersom platsbytet är säkert. Vid ett platsbyte Vi<–>Vk hamnar Vi på fel plats ty denna plats tillhör Vk+1. Alla sitter på fel plats med L är ett steg närmare sin plats. När L äntligen ska komma till sin plats, ska vi glömma honom/henne och börja att ordna en kortare rad.
Det kan dock hända en ”trafikstökning” där inget platsbyte till vänster om L är säkert. Detta innebär att varje Vi ska till platsen ett steg åt vänster. Desto bättre! Vi struntar i säkerheten och flyttar i tur och ordning V1<–>L, V2<–>L, V3<–>L, ... tills L kommer på sin plats. Då har även alla Vi hamnat på sina platser. Nu bara de som hade suttit till höger om L sitter i oordning. Vi får betydligt kortare rad att ordna vilket vi också gör.Ä5. Vi
betecknar med I resp. r medelpunkten
resp. radien till den inskrivna cirkeln
i triangeln ABC.
Låt ÐBAC=a (se
fig.). Vi ska visa att TBOA | AB.
Klart att AB1=AB cosa,
AC1=AC cosa.
Trianglarna B1AC1 och BAC har en
gemensam vinkel BAC samt AB1/AB=AC1/AC=cosa.
Detta innebär att dessa trianglar är likformiga med längdskalan cosa. Låt X vara en
projektion av punkten OA på AB. Då AX och ATB
är motsvarande tangentsträckor i trianglarna B1AC1
och BAC, står deras längder i samma förhållande, dvs.
AX=ATB cosa.
Låt Y vara en projektion av punkten TB på AB.
Då AY=ATB cosa.
Likheten AX=AY innebär att punkterna X och Y
sammanfaller. Av detta följer att TBOA | AB.
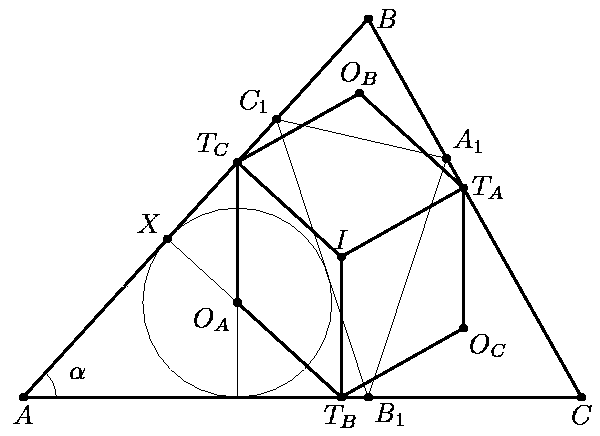
Helt analogt visar vi att
TAOB | AB, TCOB | BC,
TBOC | BC, TAOC | CA,
TCOA | CA.
Klart att ITC | AB, ITA | BC,
ITB | CA samt att ITA=ITB=ITC=r.
I fyrhörningen TBOATCI är motsatta
sidor parallella, således är TBOATCI
en parallellogram i vilken ITB=ITC=TBOA=TCOA=r.
Helt analogt får vi att TCOB=TAOB=TAOC=TBOC=r,
vilket innebär att alla sidor i sexhörningen TAOCTBOATCOB
ar lika med r.
Ä6. Låt oss måla kort av varje färg i sin egen färg. Då ska rutnätet se ut som en bild bestående av färgade fläckar. Om två kort av samma färg har en gemensam sida ingår de i samma fläck.
Låt oss visa ett antal egenskaper hos fläckar.
Lemma 1. Låt 4 kort A, B,C,D har ett gemensamt hörn (se fig.). Om två motsatta kort A och C är av samma färg f då är även kort B och D av färg f.
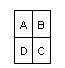
Bevis till lemma 1. Kort B ligger intill både A och C. Då A och C har olika valörer måste B ha samma färg med minst ett av korten A och C. Således har B färgen f, samma gäller D.
2. Varje fläck är rektangulär.
Klart att en fläck är en polygon vars inre vinklar är antingen 90° eller 270°. Det andra fallet är dock omöjligt. Vid en sådan inre vinkel skulle finnas tre kort av samma färg, två av de skulle vara motsatta, och då även det fjärde kortet skulle ha samma färg enligt lemma 1.
3. Två fläckar har inga gemensamma hörn.
Vid ett sådant hörn skulle finnas två motsatta kort av samma färg, vilket enligt lemma 1 skulle medföra att fläckarna sammansmältas i en.
4. Ett gemensamt hörn till två fläckar kan inte ligga på en annans fläck sida.
Låt på figuren A och B har samma färg, medan A, C och D har olika färger. Då skulle A och D, D och C samt C och B ha samma valörer, vilket innebär att A och B har samma färg och samma valör. Motsägelse.
5. Gränser mellan fläckar är sträckor som går från kant till kant.
Detta följer från egenskaper 2 till 4 och innebär att fläckar bildar ett rektangulärt nät bestående av såväl vågräta remsor som lodräta band, se fig. Bland annat innebär detta att remsor har samma höjder som fläckar vid vänstra kanten.
Det kan finnas 1 till 4 remsor. Låt oss betrakta varje möjlighet separat.
Antag att det finns exakt en remsa, då har den höjden 4. Men då är även varje fläck höjden 4, vilket innebär att antalet kort såväl i en fläck som i en färg är delbart med 4. Dock är 13 ej delbart med 4.
Antag att det finns exakt två remsor, då skulle färgfördelning se ut så här:
![]()
dvs. 4 färger i två vänstra band är olika, i det tredje bandet finns två färger som saknas i det andra bandet osv. Vi ser att färgparen (a,b) och (c,d) turas om i banden. Då höjden av varje band är 4, blir antalet kort av färgerna a och b sammanlagt delbart med 4, således kan det inte vara 26. Motsägelse.
Antag att det finns exakt tre remsor. Det kan finnas två eller tre olika färger i det vänstra bandet. Fallet med enbart två färger är helt analogt med det föregående fallet: färgparen (a,b) och (c,d) turas om i banden och antalet kort av färgerna a och b sammanlagt skulle vara delbart med 4. I fallet med tre färger i det vänstra bandet skulle färgfördelning se ut så här:
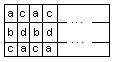
Låt de sammantagna bredderna av b-fläckar och d-fläckar är x resp. y. De fläckarna har samma höjd h, således är antalen kort av färg b och d lika med xh resp. yh. Å andra sidan är x och y heltal och x+y=13, således x¹y och xh¹yh. Motsägelse.
Återstår bara fallet med 4 remsor. Då skulle varje remsa ha höjd 1. Detta medför att varje två lodrätt intilliggande kort skulle vara av olika färg, således av samma valör. Då skulle varje två vågrätt intilliggande kort vara av olika valör, således av samma färg. VSB.Ä7. Beteckna med R talet √3. Låt a=2+R, b=3(2+R). Betrakta talet A=(2+R)m+(2–R)m. I uttrycket kancelleras samtliga udda potenser av R medan jämna potenser ger heltal som är delbara med 3. Då första termerna är lika tvåpotenser, är A ett heltal som är ej delbart med 3. Det är klart att [am]= [(2+R)m] = A–1 eftersom 0<2–R<1.
Betrakta nu talet B=3n(2+R)n +3n(2–R)n. Det är klart att B är ett heltal som är jämnt delbart med 3. Då även 3(2–R)=3/(2+R)<1, gäller att [bn]= [3n(2+R)n] = B–1.
Likheten [am]= [bn] skulle medföra att A=B, vilket är omöjligt då B är delbart med 3 medan A inte är det.Ä8. Då extravisaren pekar på mittpunken i bågen mellan tim- och minutvisarna, rör extravisaren sig med vinkelhastigheten som är aritmetiskt medelvärde av vinkelhastigheter hos de två visarna. Minutvisaren rör sig med hastigheten 1 varv/tim, timvisaren med 1/12 varv/tim, således extravisaren med 13/24 varv/tim. Under 24 timmar gör extravisaren således 24/(13/24)=13 varv.
Ä9. Då schackbrädet består av ett udda antal rutor skulle det finnas även en delrektangel som omfattar ett udda antal rutor. Sidorna x och y hos denna rektangel skulle då vara udda tal. Då är summan x+y ett jämnt tal, således är omkretsen 2(x+y) delbart med 4.
Ä10. Vi markerar alla rader på vilka står exakt en pjäs. Om samtliga horisontella rader vore markerade skulle detta innebära att det står exakt 8 pjäser på brädet. Således är högst 7 horisontella rader markerade. Samma gäller vertikala rader. Detta medför att sammanlagt är högst 14 rader markerade, på vilka står högst 14 pjäser. Då finns det en pjäs som inte står på någon markerad rad. Detta innebär att såväl i den horisontella som i vertikala raden står den pjäsen inte ensam och kan således tas bort.