Your total score is based on the three problems for which you earn the most points; the scores for the individual parts of a single problem are summed. Points for each problem are shown in brackets [ ].
1. [3] The little squares of an n by n table are filled with numbers, all of which are different. The smallest numbers in each row were marked, and it turned out that all the marked numbers were in different columns. Then the smallest numbers in each column were marked, and it turned out that these marked numbers were in different columns. Show that both times the same numbers were marked.
2. [3] Between two parallel lines there is a circle of radius 1, tangent to both lines, and an isosceles triangle, whose base lies on one of the lines and whose vertex is on the other. It is known that the triangle and the circle have exactly one common point, and this point lies on the inscribed circle of the triangle. Find the radius of the inscribed circle.
3. [4] The natural numbers a,b,c,d are such that their least common multiple equals a+b+c+d. Prove that abcd is divisible by 3 or by 5 (or by both).
4. [4] The squares of an 8 by 8 chessboard are not colored yet. How many colorings of the board's squares in black and white are there such that 31 squares are black and no two of black squares have a common side. (Indicate the number of colorings and prove that all the possibilities have been taken into account; two colorings are considered different if there is at least one square which is black in one coloring and white in the other.)
5. [6] A weight of 11111 grams is placed on the right-hand plate of a balance. Someone places weights on the two plates of the balance; the first weight is 1 gram, and each successive weight is twice as heavy as the previous one. At some moment the two plates are in equilibrium. Where was the 16 gram weight placed (on the left or on the right)?
6. [7] In the spring round of the Tournament of Towns this year 6 problems were proposed to upper grade pupils of country N. Each problem was solved by exactly 1000 such participants, but no two participants (taken together) succeeded in solving all 6 problems. What is the smallest possible number of upper grade participants from country N in the spring round? (Indicate this number, show that for this number the conditions of the problem can be met, and cannot be met for a smaller number.)
7. [8] A first grade student has 100 cards on which the integers 1 to 100 are written, as well as a sufficiently large number of cards on which the symbols + and = appear. What maximal number of true equalities can he constitute? (Each card is used no more than once. The sign "=" can be used only once in any equality obtained by the student. In order toget a new number the student cannot rotate the cards or place any two cards with the numbers together.)
1. [3] The natural numbers a,b,c,d are such that their least common multiple equals a+b+c+d. Prove that abcd is divisible by 3 or by 5 (or by both).
2. [4] For what largest integer n can we find n points on the surface of the cube, not all lying on one face and forming the vertices of a regular plane n-gon.
3. [4] The side lengths of triangle ABC are known: AB = c, BC = a, CA = b, and a<b<c. Two points B' and A' are chosen on the rays BC and AC respectively so that BB'=AA'=c. Two points C" and B" are chosen on the rays CA and BA so that CC" = BB" =a. Find the ratio of the segment A'B' to the segment C"B".
4. Suppose that nonzero integers a1, a2, ... , an satisfy the equation
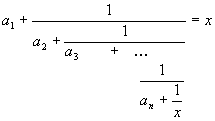
for all values of x for which the left-hand side of the equation makes sense.
(a [3]) Prove that the integer n is even.
(b [4]) For what least n do such numbers exist?
5. [6] The little squares of an m by n table are painted in two colors. It is known that if a rook is placed on any square, it will attack less squares of the same color (that of the square it is placed on) than squares of the other color. (A rook attacks all the squares in the row and in the column it is placed on, including the one it stands on.) Prove that in each row and in each column the number of squares of one color is the same as that of the other one.
6. (a [5]) Several black squares of side 1 cm are nailed to a white plane by means of a nail of thickness 0.1 cm; they form a black polygonal figure. Can the perimeter of this figure be 1 km long? (The nail cannot touch the boundary of any square.)
(b [5]) Same problem, but with a nail of thickness 0 (a point).
(c [5]) Several black squares of side 1 lie on the white plane, forming a black polygonal figure (possibly having more than one piece and/or having holes). Can the ratio of its perimeter to its area be more than 100000?