Lektion 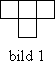19 Upprepade mönster och symmetri

1. Figuren på bilden heter T-tetramino. Hur kan man bilda en kvadrat av 100 sådana figurer?

2. På hur många sätt kan man vrida och vända figuren så att den upptar exakt samma plats? Figuren kan vara a) en rektangel; b) en kvadrat; c) en triangulär halva av en kvadrat; d) en cirkel?

3. Indela en kvadrat a) i två likadana sexhörningar; b) i två likadana femhörningar;
c) i fyra likadana 8-hörningar.

4. 11 brickor är utplacerade på ett schackbräde spegelsymmetriskt kring en av huvuddiagonalerna. Visa at det finns minst en bricka på denna huvuddiagonal.

5. En bonde ville köra en get, en kål och en varg över en flod. Båten rymmer honom och endast ett av djuren eller kålen. Om bonden lämnar djuren utan tillsyn då äter geten upp kålen eller äter vargen upp geten. Ända lyckades bonden köra allt och alla över floden intäckta. Visa att det fanns ytterliggare ett sätt att göra detta.

6. En turist måste promenera från ett tält till en lägereld samt hämta en hink vatten från en flod under promenaden. Vi antar att positioner av tältet och lägerelden är kända samt att stranden är rak. Vilken väg skall turisten välja för att den blir så kort som möjligt?

den 22 mars 2003, Sonja Kovalevsky-skolan , Mattecirkel, http://shap.homedns.org/sks/svenska/