А.В.Шаповалов => Олимпиады и турниры => Турнир им. Савина

Избранные задачи

Журнал Квантик 2012, №8

Задачи сгруппированы по тематическим разделам, в скобках после номера – классы, для которых предлагалась задача, курсивом указаны авторы задач.

АЛГЕБРА

1. (6) Астролог считает год счастливым, если в его записи используются четыре последовательные цифры. Например, следующий, 2013-й год будет именно таким. А когда, по мнению этого астролога, был предыдущий счастливый год? (Н. Нетрусова)

2. (6-7) За одно нажатие можно число на экране калькулятора увеличить на его дробную часть (например, из ³/₇ можно получить ⁶/₇, а из 3,8 получить 3,8 + 0,8 = 4,6). Начав с положительного числа, меньшего 1, за десять нажатий получили число 10. С какого числа начали? (А. Шаповалов)

3. (7) Среднее арифметическое всех Володиных оценок по геометрии за четверть – целое число. Если заменить все двойки – тройками, тройки – четверками, а четверки – пятерками, то среднее арифметическое оценок опять-таки будет целым. Что Володя получил в четверти, если известно, что первая оценка у него – двойка, а последняя – четвёрка? (В. Гуровиц)

4. (6-8) Каждая цифра натурального числа N строго больше стоящей слева от нее цифры. Чему равна сумма цифр числа 9N? (С. Волченков)

ГЕОМЕТРИЯ

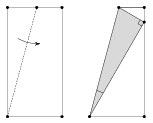
5. (7) Квадратный лист бумаги сложили вдвое, а затем так, как показано на рисунке. Чему равен отмеченный угол? (Д. Шноль)

КОМБИНАТОРНАЯ ГЕОМЕТРИЯ

6. Докажите, что любой треугольник можно разрезать на три меньших треугольника так, чтобы каждую из получившихся частей можно было покрыть двумя другими. (А. Шаповалов)

КОМБИНАТОРИКА

7. (6-7) Разложите 100 орехов на 10 кучек так, чтобы в них было разное число орехов, но но никакую из куч нельзя было бы разбить на две так, чтобы получилось 11 кучек с разным числом орехов. (А. Шаповалов)

8. (6-7) На клетчатой доске стоят 4×10 стоят 7 слонов. Докажите, что можно поставить восьмого слона так, чтобы он никого не побил. (А. Шаповалов)

9. (6-7) Перед Петей и Васей лежат кучки по 100 монет. Они ходят по очереди, начинает Петя. За один ход можно взять из чужой кучки одну или несколько монет и переложить в свою кучку. Каждым ходом надо перекладывать новое число монет. Кто не может сделать ход – проиграл. Кто из них может выиграть, как бы ни играл соперник? (А. Шаповалов)

10. (6-8) Ире принесли 7 драгоценных камней разного веса. Прибор «РИВ-6» умеет за одно испытание из шести камней выбрать два средних по весу. Как за 5 испытаний Ира сможет найти самый средний по весу камень из семи? (В.Трушков, И.Руденко)

11. (7-8) Девять гномов трижды становились по одному в клетки квадрата 33, и каждый раз гномы, оказавшиеся в соседних по стороне клетках, здоровались. Докажите, что какие-то два гнома так и не поздоровались. (А. Грибалко)

12. (7-9) Большая свеча сгорает за час и стоит 60 рублей, а маленькая сгорает за 11 минут и стоит 11 рублей. Можно ли отмерить минуту, затратив не более, чем 150 рублей? (А. Шаповалов, Л. Медников)

ЛОГИКА

13. (6-7) Было 12 карточек с надписями «Слева от меня – ровно 1 ложное утверждением», «Слева от меня – ровно 2 ложных утверждения», …, «Слева от меня – ровно 12 ложных утверждений». Петя разложил карточки в ряд слева направо в каком-то порядке. Какое наибольшее число утверждений могло оказаться истинными? (А. Шаповалов)

14. (6-7) Шесть незнакомых между собой жителей острова рыцарей и лжецов поужинали за круглым столом при свечах, так что каждый из них разглядел и запомнил только двух своих соседей по столу. Назавтра, одному из них – Артуру, захотелось узнать, кто сидел напротив него. Он может за один вопрос узнать у любого про любого другого (кроме себя), спросив: «Сидел ли тот рядом с тобой за ужином?». Хватит ли Артуру четырёх вопросов?
(А. Шаповалов)